Last year, I had the opportunity to take a software security & exploitation course by the amazing Vasileios Kemerlis. We learned about everything from JIT code reuse to tool-chain based hardening and kernel exploitation, but something that really caught my attention was the idea of shellcode.
Specifically, there was this one extra credit opportunity where we were simply told to make two of our previous exploits not just null-free, but alphanumeric. This was my introduction into the wacky world of alphanumeric shell code and I feel like I learned a lot throughout the process, so I’d love to share it.
I’m not going to go too deep into the actual code I wrote (partially bc I’m TAing the course in the fall and don’t want to be responsible for accidentally leaking answers)– I’ll focus more on the process and conceptual approach that ended up working for me!
Editor’s Note: Everything here is for the IA-32 instruction set on Linux. I think a lot would transfer to x86-64 too, but this class’ projects focused on 32-bit to make exploit & address sizes more manageable.
Building My First Alphanumeric Shellcode
For most of the semester (this project came up about halfway in), my approach to writing shellcode had been pretty simple–just use my notes to write out x86 assembly for what I wanted the exploit to do and then use an online compiler to translate that to a machine code payload.
However, this strategy wouldn’t work for writing alphanumeric because alphanumeric characters account for only (wait hold on 26 lowercase + 26 uppercase + 10 numbers…) 62 of the 256 possible byte values we can use in normal shellcode. Unlike before where I was just constrained by a poor understanding of assembly, now I was also constrained by only being able to use a small subset of instructions and numbers.
| char | bytes | instruction | char | bytes | instruction | char | bytes | instruction | char | bytes | instruction | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | \x41 | inc %ecx | Q | \x51 | push %ecx | g | \x67 | [16b addr sz] | w | \x77 | ||||
| B | \x42 | inc %edx | R | \x52 | push %edx | h | \x68 | pushl $0x.. | x | \x78 | ||||
| C | \x43 | inc %ebx | S | \x53 | push %ebx | i | \x69 | y | \x79 | |||||
| D | \x44 | inc %esp | T | \x54 | push %esp | j | \x6a | pushb $0x.. | z | \x7a | ||||
| E | \x45 | inc %ebp | U | \x55 | push %ebp | k | \x6b | 0 | \x30 | xor | ||||
| F | \x46 | inc %esi | V | \x56 | push %esi | l | \x6c | 1 | \x31 | xor | ||||
| G | \x47 | inc %edi | W | \x57 | push %edi | m | \x6d | 2 | \x32 | xor | ||||
| H | \x48 | dec %eax | X | \x58 | pop %eax | n | \x6e | 3 | \x33 | xor | ||||
| I | \x49 | dec %ecx | Y | \x59 | pop %ecx | o | \x6f | 4 | \x34 | xorb $0x.., %al | ||||
| J | \x4a | dec %edx | Z | \x5a | pop %edx | p | \x70 | jo $0x.. (rel) | 5 | \x35 | xorl $0x.., %eax | |||
| K | \x4b | dec %ebx | a | \x61 | popad | q | \x71 | 6 | \x36 | |||||
| L | \x4c | dec %esp | b | \x62 | r | \x72 | 7 | \x37 | aaa | |||||
| M | \x4d | dec %ebp | c | \x63 | s | \x73 | 8 | \x38 | cmp | |||||
| N | \x4e | dec %esi | d | \x64 | t | \x74 | 9 | \x39 | cmp | |||||
| O | \x4f | dec %edi | e | \x65 | u | \x75 | ||||||||
| P | \x50 | push %eax | f | \x66 | [16b operand sz] | v | \x76 |
Looking at the table above, you can see that we can actually still dec and pop into all eight x86 registers plus we can inc and push from most of them (horayyy!). But the absolute life-savers that make this whole idea work are the pair of XOR instructions (for bytes and dwords) that we can use to build numbers that aren’t originally allowed.
Undaunted, I just started from the beginning, taking my code for the first exploit and rewriting it with semantically equivalent instructions from the limited set. My initial exploit had mov $0x14, %eax? Well, we can’t use the \xb8 for mov, but we can just push $0x14 and then pop %eax. But we can’t use the value $0x14 either, so instead we can do push $0x55, pop %eax and then that life-saving xor $0x41, %al–all to get $0x14 back into %eax without using non-alphanumeric characters1.
After a little while it was time to make a syscall. Function arguments in x86 are pushed onto the stack, which at first seems perfect for us because we have hella push instructions. Unfortunately, arguments for syscalls are passed in registers instead, with the call number for the one to make in %eax, the first arg in %ebx, and so on.
Remember when I was excited about being able to push and pop to get values into most registers as a replacement for mov? Turns out there is one notable exception – you can’t pop into %ebx. So either we stick with only making the syscalls that don’t take any arguments (none of the fun ones), or we’ll have to find another way to load values into %ebx.
Popad to The Rescue
popad (‘pop all dword’), is an assembly instruction I’d never used before and honestly don’t fully understand (how often do you really need to pop into all 8 general purpose registers in a row??). That being said, it does exactly what it says; it pops all. And this turns out to be the only2 alphanumeric way to load new values into %ebx.
popad is actually the companion to the pushad (‘push all dword’) instruction and together they were initially introduced back in the ’80s to allow processors to store the state of their registers on the stack and then restore them at a later point. So pushad basically pushes all 8 general registers in order3 onto the stack–%eax, %ecx, %edx, %ebx, original %esp, %ebp, %esi, and %edi. And then later, popad pops them off in the opposite order to restore all of their values (except for the original %esp4).
So, even though pushad doesn’t happen to be one of the alphanumeric instructions, we can mimic it by pushing all 8 registers in the same way that it would, but pushing the value we want to move into %ebx when we would normally push %ebx itself. Thus, if we call popad right after, every register will be reset to its value before we did all the pushing except for %ebx, which will be set to the new value.
And this strategy is actually pretty convenient because not only do we now have a way to load our first syscall argument %ebx, but we can use the same popad call for any other arguments we need to load by pushing specific values instead of %ecx, %edx, or others during the simulated pushad!
But hold on… How the hell are you supposed to even make the syscall? The exploit we had to make for class wasn’t crazy complicated but it still required you to write a string to a file and then kill the process. In order to do either of those things you’d need a kernel interrupt from int $0x80 (\xcd\x80 in bytes) at least a couple times and that’s not alphanumeric…
Reconstructing Shellcode
After some confused googling I came across a great article by Russell Sanford which had the genius idea of using an initial alphanumeric shellcode to push code onto the stack for another final shellcode that would actually do our exploit. So for example, since we can’t use the int $0x80 instruction in our initial shellcode, we can instead have that initial shellcode somehow reconstruct the bytes \xcd\x80 and push them onto the stack, so that we can eventually run those bytes as code anyway!
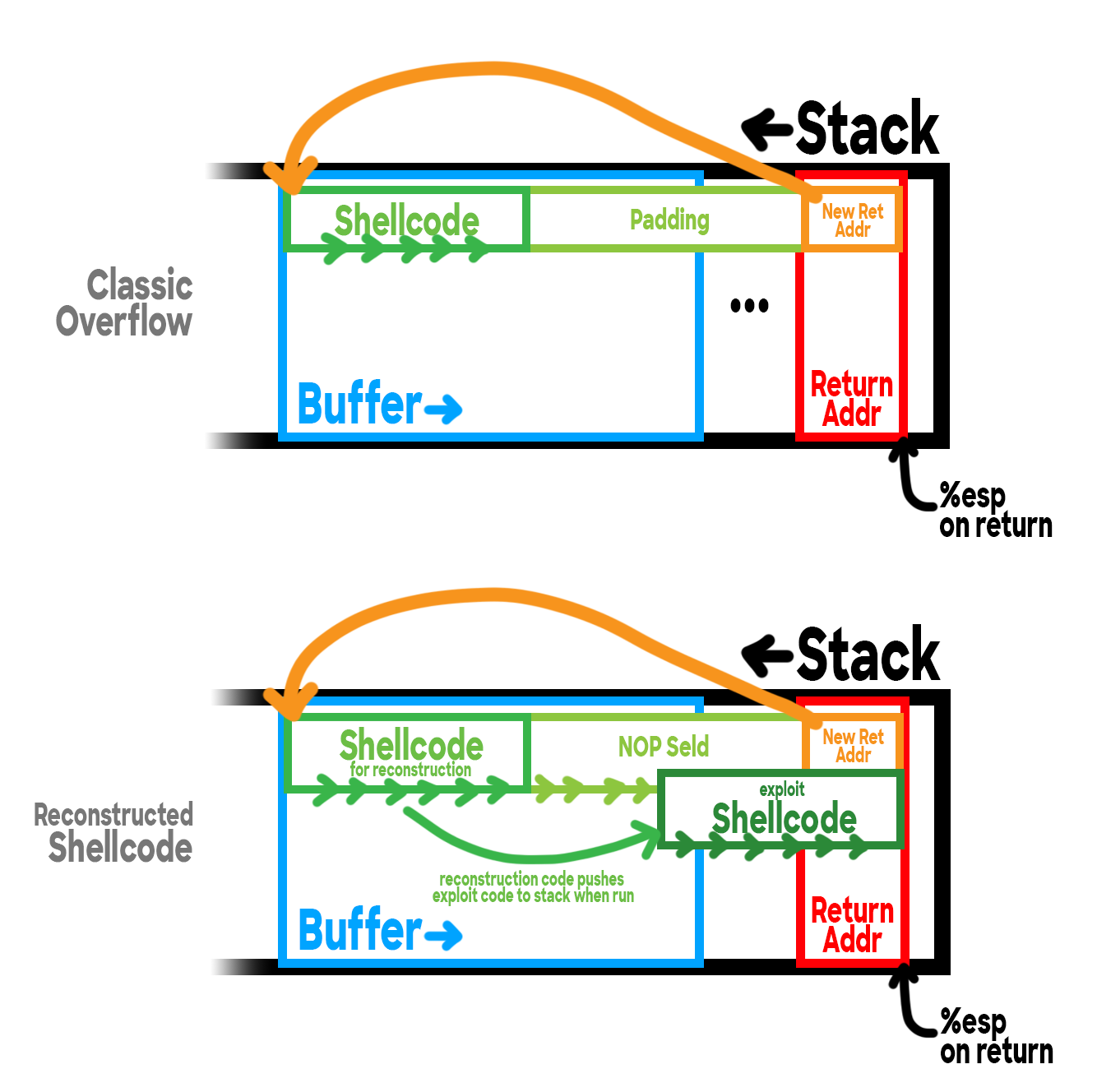
In a classic buffer overflow attack, you write your shellcode into the buffer followed by some padding, and a pointer to overwrite the function’s return address. This way, when the function that read into the buffer returns, it will erroneously return to the start of your shellcode and begin execution there.
And our new reconstructed shellcode strategy does basically the same thing: still starting with some shellcode in the buffer followed by padding and overwriting the return address. However, the difference is that our first ‘reconstruction’ shellcode isn’t meant to actually perform the exploit, but its whole goal is to reconstruct the non-alphanumeric bytes \xcd\x80 (corresponding to int $0x80) that we need to do the exploit. Once it has those bytes, it will push all of the final exploit code I’d been writing so far onto the stack, inserting those syscall bytes wherever they’re needed.
After the reconstruction shellcode finishes running, we just have to make sure we don’t return so that execution will continue along the nop sled5 until it reaches our newly reconstructed shellcode and continues execution from there!
Not only that, but one final twist is that the final exploit code has to be pushed onto the stack totally backwards.
Pushing the Shellcode onto the Stack
If you think about it logically, the stack grows from higher addresses to lower addresses, but the %eip instruction pointer that controls execution runs from lower addresses to higher ones. This means that if we were to call push $0xaabbccdd and then push $0x11223344, the latter set of bytes would be stored at a lower memory address and thus be the first to be encountered and run by the instruction pointer.
Not only that, but due to the little endianness of the x86 architecture, the byte \x44 would actually be the very first byte to be encountered and interpreted as code. So, if we want to push the shellcode bytes \x11\x22\x33\x44\x55\x66\x77\x88, we would have to first do push $0x88776655 and then push $0x44332211 in order to make sure they are pushed in the correct order to be interpreted.
Note: the pushb instruction is actually not alphanumeric (although pushw luckily is, so if your desired final shellcode ends up being an odd number of bytes (like mine was), you can just add another nop equivalent byte to the start so it can be pushed with just those instructions!
Conclusion
Now is this a very contrived situation? Probably. Would any real piece of software so strict about you inputting only alphanumeric characters definitely have ASLR, canaries, or a whole host of other protections that’d make this attack useless? I think so. But was this a very fun challenge that taught me tons about assembly and kinda blew my mind with code re-writing itself as it runs? Yes, it was. And I always appreciate problems that capture my attention so wholly and deeply as this one did–they’re a special kind of experience.
I’ll leave you with this: j0X40PZHf5A0f5sOfPhRX4Bh4bPYhUVWahjgPThjhjZfPhUX4AfhAjAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAê¥ˇø6
The $0x55 and $0x41 pair here is totally arbitrary, in theory you can use any values that fall within the alphanumeric range and XOR to your desired value (I used this calculator a ton to find ones that worked for more complex register values). And if you can’t find any that work you can always just do a chain of 3 or more XORs to get what you need out of the values you can use.
At least I think so… Maybe there’s an angle where you zero %ebx and then use inc %ebx over and over until you get to the value you need. But even then, zeroing %ebx is difficult without xor %ebx, %ebx unless you somehow already know what’s in it.
I was always confused about why the order of registers was %eax, %ecx, %edx and then %ebx because its not alphabetical?? Didn’t the inventors of x86 know that b comes before c?? It turns out its because they all have full names that make more sense in this order.
Which makes sense because the stack pointer would have changed during the push operations.
Although the nop instruction itself isn’t alphanumeric (it’s 0x90), there are actually a ton of great alphanumeric options for NOP sleds–I found this article extremely helpful. In my case, I just used inc %ecx (\x41 or A) which was essentially a nop because I reset the %ecx register very early in my shellcode anyway. Plus all the AAAAs looked like screaming and that was about how I felt by this point.
Yes, I know, the last four characters aren’t actually alphanumeric, but that’s because only the payload had to be alphanumeric for the extra credit. I don’t make the rules.